Strange Errors, Makefiles, and Large Matrices

Sep 29, 2010 · 3 minute read · Comments
C CUDA Makefiles

Strange Errors Abound

The first problems I encountered numbered in the hundreds. I was getting errors that all said something like this:

error: expected ‘=’, ‘,’, ‘;’, ‘asm’ or ‘attribute’ before cut…

After some frantic Google searching (yes, it worked this time) I came across a forum thread that contained some lists of error messages that seemed similar to mine. Someone in this thread suggested that the compiler was compiling the CUDA code as C code so the standard library of CUDA functions was not automatically being referenced. The solution to this problem (obviously enough) is to put the file extension .cu at the end of any file that contains CUDA library function calls or any CUDA specific syntax like so:

file_with_cuda_stuff.cu

Makefiles for CUDA

When compiling a CUDA program that has multiple files, it is best to create a makefile that can do this work for you instead of having to manually type in every command every time. There is a CUDA makefile format that includes all sorts of options, including:

EXECUTABLE
CUFILES
CUDEPS
CCFILES
LIBS
LDFLAGS
INCLUDES

These are supposedly all you need to create a makefile for a CUDA program, with the line

include /path/to/common.mk

at the end to include all of the standard options that come with the CUDA SDK.

I had a lot of problems using this kind of makefile; the LDFLAGS and LIBS options were failing to pass through and I had absolutely no idea why. What I decided to do next was use a regular makefile, as I had some experience with these while writing C and C++ programs in the past. This did the trick. Without all of the options and complexity (which I’m sure comes in handy to someone at some point) it is a much simpler and cleaner makefile. Example:

# Awesome Makefile
proj.out : proj.cu
    nvcc proj.cu -I/opt/cuda-sdk/C/common/inc -L/opt/cuda-sdk/lib

Large Matrix Multiplication

Background

I recently had to write a program (read: do a homework assignment) that multiplied two large matrices. One was 8192 x 32768 and the other was 32768 x 32768. Both contained 32 bit single precision floating point numbers.

The Basic Idea

When you can’t fit the operand matrices and the result matrix in memory in their entirety, you must split them up in a way that still enables tiling and maximizes occupancy of the multiprocessors inside the chip. The way you can split up the input and output matrices can be seen in this picture:

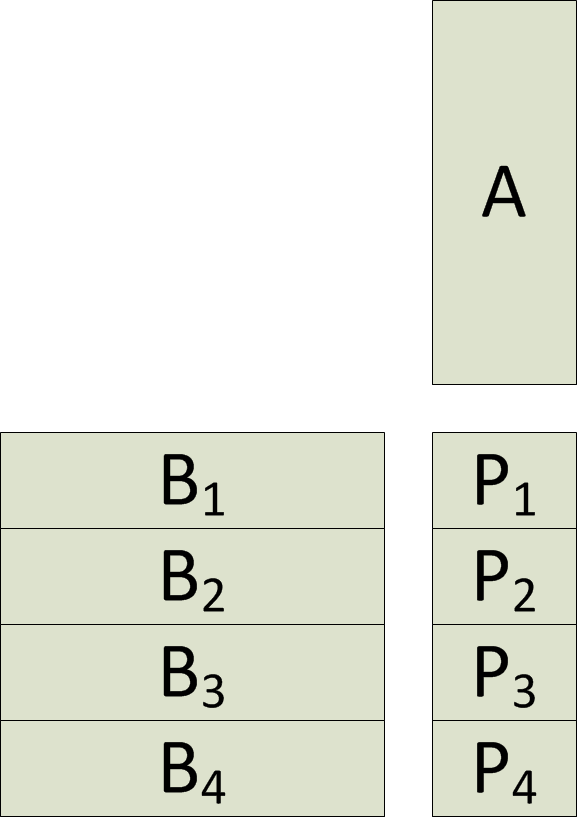
Breakdown of matrices

You take a strip out of each matrix that, when multiplied by the other, gives you the section of the result matrix that you want. This division and joining happen on the host computer, not on the device. The device memory can only hold the partitions that you move on to the device at one time. When you need to multiply the next chunk, you overwrite the current strip that is on the device. Each pair of matrix strips is a separate kernel launch, each of which requires moving the operands and result to and from the device. In the end, the results can be stitched back together on the host.

Scott Mansfield